Formeln Dreieck: Unterschied zwischen den Versionen
Aus Wiki.sah
E.T. (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
|||
| (15 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
Im rechtwinkligem Dreieck ist die Summe der Quadrate über den Katheten gleich groß, wie das Quadrat über der Hypotenuse. Im nachfolgenden Bild ist der Rechte Winkel der an Ecke C des Dreiecks. | Im rechtwinkligem Dreieck ist die Summe der Quadrate über den Katheten gleich groß, wie das Quadrat über der Hypotenuse. Im nachfolgenden Bild ist der Rechte Winkel der an Ecke C des Dreiecks. | ||
http://www.science-at-home. | http://www.science-at-home.de/bilder/wikidata/mathematik/rechtwinkliges_dreieck_01.gif | ||
{| | {| | ||
| Zeile 81: | Zeile 81: | ||
== Winkelfunktionen == | == Winkelfunktionen == | ||
{{Adsense responsive}} | |||
http://www.science-at-home. | http://www.science-at-home.de/bilder/wikidata/mathematik/rechtwinkliges_dreieck_02.gif | ||
{| | {| | ||
| Zeile 134: | Zeile 134: | ||
c Hypotenuse | c Hypotenuse | ||
== Sinussatz == | |||
{| | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#e1e8f2" align="center" valign="middle" | |||
|a : b = sin α : sin β | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''a''' = (sin α · b) / sin β | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''b''' = (sin β · a) / sin α | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''sin α''' = (sin β · a) / b | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''sin β''' = (sin α · b) / a | |||
|} | |||
|} | |||
{| | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#e1e8f2" align="center" valign="middle" | |||
|b : c = sin β : sin γ | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''b''' = (sin β · c) / sin γ | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''c''' = (sin γ · b) / sin β | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''sin β''' = (sin γ · b) / c | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''sin γ''' = (sin β · c) / b | |||
|} | |||
|} | |||
{| | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#e1e8f2" align="center" valign="middle" | |||
|c : a = sin γ : sin α | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''c''' = (sin γ · a) / sin α | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''a''' = (sin α · c) / sin γ | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''sin γ''' = (sin α · c) / a | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''sin α''' = (sin γ · a) / c | |||
|} | |||
|} | |||
== Kosinussatz == | == Kosinussatz == | ||
| Zeile 153: | Zeile 237: | ||
|} | |} | ||
== Fläche/Umfang == | |||
http://www.science-at-home.de/bilder/wikidata/mathematik/dreieck.gif | |||
{| | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#e1e8f2" align="center" valign="middle" | |||
|'''A''' = (l<sub>1</sub> · b) / 2 | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''l<sub>1</sub>''' = (A · 2) / b | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''b''' = (A · 2) / l<sub>1</sub> | |||
|} | |||
|} | |||
{| | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#e1e8f2" align="center" valign="middle" | |||
|'''U''' = l<sub>1</sub> + l<sub>2</sub> + l<sub>3</sub> | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''l<sub>1</sub>''' = U - (l<sub>2</sub> + l<sub>3</sub>) | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''l<sub>2</sub>''' = U - (l<sub>1</sub> + l<sub>3</sub>) | |||
|} | |||
| | |||
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center" | |||
|- bgcolor="#edecf2" align="center" valign="middle" | |||
|'''l<sub>3</sub>''' = U - (l<sub>1</sub> + l<sub>2</sub>) | |||
|} | |||
|} | |||
A Fläche | |||
l<sub>1</sub>, l<sub>2</sub>, l<sub>3</sub> Längen der Seiten | |||
b Breite | |||
U Umfang | |||
---- | |||
'''Pfad: [[Hauptseite|Home]] / [[Mathematik]] / [[Formeln Geometrie|Geometrie]] / [[Formeln Dreieck|Dreieck]]''' | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Formel Geometrie]] | |||
[[Kategorie:Ad man]] | |||
Aktuelle Version vom 12. Februar 2024, 17:27 Uhr
Allgemeine Eigenschaften

Bennennung der Eckpunkte
|
A, B und C (normalerweise im Uhrzeigersinn) |
|---|---|
| 180° | |
Bennennung der Winkel
|
α (am Eckpunkt A), β (am Eckpunkt B) und γ (am Eckpunkt C) |
Benennung der Seiten
|
Die Seiten werden nach dem Eckpunkt benannt mit Kleinbuchstaben, die ihnen gegenüber liegen. |
Satz des Pythagoras
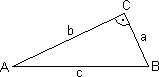
Im rechtwinkligem Dreieck ist die Summe der Quadrate über den Katheten gleich groß, wie das Quadrat über der Hypotenuse. Im nachfolgenden Bild ist der Rechte Winkel der an Ecke C des Dreiecks.
|
|
|
|
|
|
a Kathete b Kathete c Hypotenuse
Kathetensatz

Das Quadrat über a ist flächengleich zum Rechteck mit den Seiten p und c, und das Quadrat über b ist flächengleich zum Rechteck mit den Seiten q und c.
| a2 = p·c |
| b2 = q·c |
Höhensatz

|
Der Höhensatz besagt, dass in einem rechtwinkligen Dreieck das Quadrat über der Höhe flächengleich dem Rechteck aus den Hypotenusenabschnitten ist. |
| h2 = p·q |
Winkelfunktionen
|
|
|
|
|
|
|
|
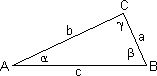
a Gegenkathete von α, Ankathete von β b Gegenkathete von β, Ankathete von α c Hypotenuse
Sinussatz
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kosinussatz
| a² = b² + c² - 2bc · cos α |
| b² = a² + c² - 2ac · cos β |
| c² = a² + b² - 2ab · cos γ |
Fläche/Umfang
|
|
|
|
|
|
|
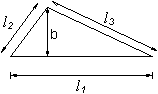
A Fläche l1, l2, l3 Längen der Seiten b Breite U Umfang
Pfad: Home / Mathematik / Geometrie / Dreieck